Monthly Archives: July 2016

மூத்தோர் பெருமை, தடுமாறும் அறிவியல் மற்றும் கணித வரலாறு

Posted on by
4

வர வர நம்மாட்களிடம் முன்னோர்களின் பெருமைகளையெடுத்துச் சொல்லவே பயமாகத் தான் உள்ளது. பார்த்தியா… என ஆரம்பித்துவிடுகிறார்கள்.. விவசாய விஞ்ஞானியான நண்பர் பிரபு  கணக்கதிகாரம்[1] பற்றியத் தகவலைப் பகிர்ந்திருந்தார்.   அவர்தம் பகிர்வுகள் எப்பொழுதும் அலறும் அறிவியல் உண்மைகளோடும் உசாத்துணைகளோடும்  எக்காளத்துடனும் நையாண்டியுடனும் எள்ளலும் துள்ளலும் தூக்கலாய் இருக்கும்.   அடிப்படையில் நான் புத்தர் காலத்து தத்துவங்களிலேயே உழன்று கொண்டிருப்பவனாயினும், என்னுடையப் பார்வை, ஒரு நவீன கட்டமைப்பு குவாண்ட இயற்பியலாளனுடையது (Foundational quantum physicist).  மூத்தோர் பெருமை, மூத்தோர் ஆய்வின் தற்காலத் தேவை என சரியான அளவீட்டைத் தேட வேண்டிய அவசியம் எல்லா அறிவியலாளர்களுக்கும் உள்ளது.   இருந்தாலும், தற்பொழுது அறிவியலுக்கு ஸ்வய சேவகம் செய்பவர்களால் பெரும் தலைவலியாய் உள்ளது.  இவர்களின் ஸ்வயம் பாகத்தால் முன்னோர் விசயங்களின் மேல் வெறுப்பு மட்டுமே உண்டாகும்.  இக்கட்டுரையில் குறிப்பிட்டிருக்கும் விவாதத்தில் இதை பேராசிரியர்கள் செயபாண்டியனும் செல்வகுமாரும் குறிப்பிட்டிருந்தனர்.  இருக்கட்டும்.

ஃபிபனாக்சி விகிதம்

சற்று கூர்ந்து கவனித்தால், இயற்கையில் பெரும்பாலும் எதிரொளி/லிக்கப் படும் தெய்வீக விகிதம் என அழைக்கப்படும் பிபனாக்சி விகிதத்தை (Fibonacci or divine ratio \varphi=\frac{1\pm\sqrt{5}}{2}) எளிதாகப் பிடிக்கலாம், அவ்வழி செல்கையில், தொடர் பின்னங்கள் (Continued fraction) தானாய் வந்து அமர்ந்து கொள்ளும், தொடர் பின்னங்களை பலா முட்களின் அமைவை வைத்தும் காணவியலலாம் (இது ஓர் அனுமானமே, அனுமானமே, அனுமானமே…).

\varphi =1+ \cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{\ddots}}}}

ஆனால், சுளையின் கணக்கு, விதைகளின் கணக்குக்கு விவசாய ஆன்றோர்களால் தான் பதில் சொல்ல முடியும்.  அதே நேரம், விதைகள்/சுளைகளும் முட்களைப் போல், அழகுவழி அமையும் பட்சத்தில், சூத்திரம் அமைப்பது மிக எளிது, அதுவும் இம்மாதிரி பயன்பாட்டுக் கணக்குகள், நம்மாட்களுக்கு பலாச்சுளை! அழகியலோடு இயற்கையின் நுட்பமும் சேர்ந்தது ஆதலால், அதுவொரு குத்துமதிப்பான அளவைத் தர வாய்ப்புகள் அதிகம். (முடிவிலா மின் சுற்றும், கொஞ்சம் ஜனரஞ்சக திண்ம அறிவியலும்! இக்கட்டுரையில் மின்சுற்றுகளிலும் மற்ற இயற்பியல் அமைவுகளிலும் பிபனாக்சி விகிதத்தைக் காண முடிவதைக் காண்பித்திருந்தேன்.)

சரி கண்டுபிடித்துவிட்டோம்… அதற்கு அடுத்த படி என்ன?  சுளை எண்ணிக்கை அதிகப்படுத்தலாமா அல்லது இயற்கையை அறிவதில் அடுத்தபடிக்கு முன்னேறலாமா??  என்பதே அறிவியலைத் தூக்கிப் பிடிப்போரின் கேள்விகள்.  முதலில் ஒன்றைப் புரிந்து கொள்ள வேண்டும், அறிவியல் என்பது, கிபி 17 ஆம் நூற்றாண்டில் ஆகாயத்திலிருந்து, நியூட்டனின் தலையில் விழவில்லை.  அது எப்போதும் நம்முள் இயங்கிக் கொண்டேயிருக்கிறது,  நாம் மனிதராக இல்லாமல்,  அமீபாவாக இருந்தாலும்,  ஒரு ஒவ்வாத வேதிச் சூழ்நிலையை உணர்ந்துவிட்டால் உடனே அமீபாவான நாம் நகரத் துவங்குவதிலேயே, உடல் உந்துதலிருந்தே தேடல் ஆரம்பித்திருக்க வேண்டும்.  சரி இவ்வளவு கூட யோசிக்கத் தேவையில்லை.   முன்னோர்களே அவ்வளவு அறிவாக இருந்திருக்கிறார்களே, நமக்கு எங்கே போச்சு புத்தி எனக் கேட்டால், தேசத்துரோகி ஆக்கிவிடுகிறார்கள்.

ஒரு எடுத்துக்காட்டு

அதுவும் தேசபக்தர்களுக்கான மதஞ்சார்ந்த எடுத்துக்காட்டு, இந்தியாவில், சில பகுதிகளில் சப்த கன்னியர்/அட்ட மாதர் வழிபாட்டில், விநாயகி எனும் தேவதையைச் சேர்ப்பதுண்டு, அதை யாரோவொருவர் இன்ச்டாகிராமில் போட்டிருந்தார், அதற்கு ஒருவர், அதெப்படி விநாயகரைப் பெண்ணாக வரைந்து அவமானப்படுத்தலாம் என சண்டைக்கு வந்துவிட்டார்.   வேறு சிலர் அவ்வழிபாட்டு முறையை எடுத்துக்கூற.. பின் பிரச்சினை ஒருவாறுத் தணிந்தது..  இப்படியிருக்கிறது எல்லாம்..!  சரி அப்படியே இருந்துவிட்டுப் போகட்டும்..

இரண்டு விசயங்கள்:

  • முதலில் நாம்/இந்தியப் பண்பாட்டினர் தான், வந்தது போனது என வரையறையின்றி கடவுளராக்கக்கூடிய வல்லமையுள்ளோர் எனக் கூறுகிறோமே, புதிதாக ஒரு கடவுளை ஏற்கமுடியாதா என்ன?!
  • இரண்டாவது, தெரியாத விசயம் என ஒன்று இருக்க வாய்ப்பு உண்டு என யோசிக்கக் கூட முடியாதா, முன்னோர்கள் இதற்கு ஏதாவது சொல்லியிருப்பார்கள் என்று விடவும் முடியவில்லை..  அது தான் முன்னோர்கள் முட்டாள்கள் இல்லையென நீங்களே சொல்கிறீர்களே.  நீங்கள் சொன்னதையே நீங்கள் வழமை போல் முரண்படுகிறீர்கள் தானே!

பௌத்தயானர் சூத்திரம் –  விவாதத் தெறிப்பு!

திரும்பவொரு மூத்தோர் சொல் முதுநெல்லிக்கனி விளையாட்டு.   பௌத்தயானர் சூத்திரத்தைப் பற்றி எனக்கும் பேராசிரியர்கள் செல்வக்குமாருக்கும், செயபாண்டியனுக்கும் நடந்த விவாதங்களை[2] இங்கேக் காணலாம்.

பல தமிழ் முகநூலர்கள், பௌத்தயானரின் சூத்திரத்தையும் (ஹோமக் குண்டங்களின் அளவைக் கணக்கிடப் பயன்பட்டவை), பிதாகரஸ் சூத்திரத்தையும் ஒப்பீடு செய்துப் பகிர்ந்து கொண்டிருந்தார்கள்.  அதாவது பிதாகரஸ் சூத்திரத்தின் பெயரை எப்படி பௌத்தயானர் சூத்திரம் என மாற்றலாம் என கொஞ்ச நாள் முன்னர் இந்தியர்களின் அல்லது தமிழர்களின்-பெருமை விளையாட்டை விளையாடிக் கொண்டிருந்தார்கள்!

நானும் சில விளையாட்டுக் கணக்குகளை, இது சம்பந்தமாகப் போட்டு வைத்து மறந்துவிட்டேன், எதையோ தேடும் போது சிக்கியது! இன்னும் அழகுறவும், கணித அழகு செழிக்கவும் செய்யலாம்! ஆனால், அதை எதையுஞ் செய்யாமல், ஒரு பாமரன் போல ஒரு படத்தை இங்கே இடுகிறேன்!

ஒரு செங்கோண முக்கோணத்தின் அடிப்பக்கம், எதிர்ப்பக்கம், கர்ணம் என்பவற்றை முறையே a, b, c எனக் குறிப்பிடுவோம்.   பிதாகரஸ் தேற்றத்தின் படி, அடிப்பக்கத்தின் (a) இருபடியின் அளவீட்டையும் எதிர்ப்பக்கத்தின் அளவின் (b) இருபடி அளவையையும் கூட்டினால் அம்முக்கோணத்தின் கர்ணத்தின் (H_P) இருபடி அளவைத் தரும்.

பிதாகரஸ் சூத்திரம் : a^2 + b^2 = H_{P}^2 அல்லது \sqrt{a^2 + b^2} = H_{P}

பௌத்தயானர் சூத்திரம்: \frac{a}{2}+\frac{7}{8}b = H_{B} \,\, ;  a < b

இதில் பௌத்தயானரின் சிறப்பு,  அதுவொரு நேரியல் சமன்பாடு ஆகும்.  படிகள் அல்லது மடிகள் இல்லை.  ஆனால் மிக முக்கியமான விசயம்.   எந்தப் பக்கம் சிறியதாக இருக்கின்றதோ அதை a எனக் குறிப்போம், மற்றப் பக்கத்தை b எனக் குறித்தால்,  கர்ணத்தின் அளவை (H_B) இவ்வாறுப் பெறலாம் என்கிறார், பௌத்தயானர்.

இரண்டு சூத்திரத்துக்கும் உள்ள கர்ண அளவின் சிறுபிள்ளைத்தனமான  வேறுபாட்டின் அளவை H_{P}-H_{B} வைத்து வரைந்ததே, இந்த வண்ணப்படம்.   அதாவது சிவப்பு நிறம் பித்தாகரஸ் மற்றும் பௌத்தயானர் கர்ண அளவுகள் ஒன்றாக உள்ளதற்கான குறியீடு அவ்வளவே!  பிழைகளைப் பொறுத்து சிவப்பில் இருந்து நீலத்தை நோக்கிச் செல்லும்!

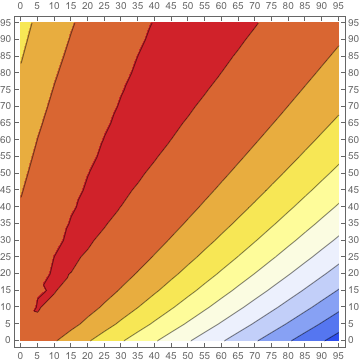
Bodhiyanar_Pythogoras.png

H_{P} - H_{B} கிடைஅச்சு – முக்கோணத்தின் அடிப்பக்கம், நேரச்சு – முக்கோணத்தின் எதிர்ப்பக்கம்

கிடை-நேரச்சுகள் இரண்டும், 1 லிருந்து 100 வரை செல்கின்றன! அவை செங்கோண முக்கோணத்தின் அடி அல்லது எதிர்ப்பக்கம்/ குத்துக் கோடுகளின் அளவுகளைக் குறிக்கிறது!

அதுவொருப் பயன்பாட்டு அளவிலாத் தொடர்பாகத் தான் காண வேண்டும்! அப்படத்தினை அணி-போன்ற வரைபடமாகப் போட்டிருந்தால் இரண்டு சூத்திரங்களின் படி பெறப்பட்ட கர்ண அளவீடுகளும்  ஒரே அளவினதாக இருக்கலாம். ( அதாவது,  H_{P} =H_{B});  ஆனால், இரண்டு அளவைகளும் ஒரே அளவினதாக இருப்பது தற்செயல் என  கணித நக்கீரனாக நாம் இருந்தால்..

இதே இருபடி-ஒருபடி வாய்ப்பாடுகளை ஒப்பிடுவதன் விளைவாய், தோராயக்கணக்கே நன்றாக இருக்கும் என இப்படியே நிறுத்தியும் விட்டேன்!

ஹோமக் குண்டத்தினை வடிவமைக்க பௌத்தயானர் பாடிவைத்தது அப்பாடல், ஆதலால், எல்லா அளவுகளையும் கணக்கில் எடுக்காமல், சில அளவுகளை மட்டுமே அவர் கருத்தில் கொண்டிருக்க வேண்டும்; அது  வசதிக்கான சூத்திரமாக மட்டுமேப் பரிந்துரைத்திருக்கப்பட்டிருக்க வேண்டும்!

எப்பொழுது எல்லாம்,  பிதாகரஸின் முவ்வெண் கோவைகளாக  (Pythagorean triples) இருக்கிறதோ சிவப்புநிறத்திற்குள் (படத்தில்) அவை வந்துவிடும், ஆனால் சில பிழைகளும் H_{P} \approx H_{B} அச்சிவப்பில் அடக்கம்! சிவனையே சினந்த மக்களின் மயக்கத்திற்கு இதுவுமொருக் காரணம்!

ஆதிசங்கரரின் ஶ்ரீசக்கரம் வரைவதற்கான சூத்திரம் மாதிரிதான் இதுவும்!  ஏன் இப்படியெனக் கேட்டால் அழகியல் கெட்டுவிடும், வேறு ஏதோ தெரியாதப் பண்புகளும் கெடலாம்!   ஆயினும் எல்லோரும் சொல்கிறார்களே, அதில் எவ்வளவு ஒத்து வருகிறது எனப் பார்த்தேன்!

தவிர, சில ஒத்துவரவில்லையெனினும் மற்றவை ஒத்து வராது என நினைப்பது, கோடலின் முழுமையற்றத்தன்மையில் அடங்கிவிடும்/விடலாம்! 😀 எண்ணியல் என்பது மிகுந்த சலிப்பையும் ஆச்சரியத்தினையும் ஒரு சேர ஊட்டும் தன்மையுடையது! அது மாதிரி ஏதாவதுத் தெரிகிறதா எனத் தேடியதன் விளைவே இக்கணக்கீடு.

எனக்கு இவை எல்லாம் — ஆகம விதிகள், சட்டுவ அளவுகள், சக்கர அளவுகள், போன்றவை –பயன்பாட்டுக்கானவற்றை மட்டும் நாம் மிகப் பிடிவாதமாக/வசதிகளுக்காக, வைத்திருந்ததன் விளைவோ என்னவோ!

இவ்விவாதத்தின் விளைவாக, ஜெயபாண்டியன் அவர்கள், பௌத்தயானர் சூத்திரத்தைப் பற்றிய சிறுகுறிப்பொன்றை வரைந்திருந்தார்.  அதை இங்கேக் காணலாம் [3].

அது மட்டும் இல்லாது,  அறிவியல் எப்பொழுதும், எவ்வளவு குழப்பமான சமன்பாடுகளைக் கொண்டிருந்தாலும், symmetry -போன்ற பண்புகள் சீராய் அமைந்து, சமன்பாட்டை எளிதாக்கிவிடும், ஆச்சரியம் என்னவெனில் சில விசயங்களில், இயற்கையும் நாம் எழுதியது போலவே, சீராய் இயங்குவதும்!    அது போல் இருபடியாய் இருப்பதை ஒருபடியாய் மாற்றுவதும் பல வகைகளில் நல்லதாக சில உதாரணங்களின் வழிக் காணலாம்!

சார்பியற் குவாண்டவியலில் நேரியலாக்கம்

நேரியல் பண்புகளோடு இருப்பது, எப்பொழுதும் நல்லது தான்!  சட்டச்சார்பிலா குவாண்டவியலின்  (non-relativistic  quantum mechanics) சுரோடிங்கரின் (Schrödinger) இருபடி சமன்பாட்டின் ஒழுங்கற்றத் தன்மையை,

[-\frac{\hbar^2}{2m} \nabla^2 + (E-V)] \psi(x,t) = -i\hbar \frac{\partial\psi(x,t)}{\partial t}

டிராக் அவர்கள், சட்டச்சார்பு கொண்ட குவாண்டவியலுக்கான நேரியற்சமன்பாடாக அல்லது ஒருபடிச் சமன்பாடு ஆக்குவதன் மூலம் தீர்வை எளிதாக மாற்ற விழைந்தார்!  முதலில் சுரோடிங்கரின் சமன்பாட்டை சார்பியலோடுக் கலந்தால் அது,

(-c^2 \hbar^2 \nabla^2 +m^2 c^4) \psi(x,t) =(-i\hbar \frac{\partial \psi(x,t)}{\partial t})^2  (இருபடி)கிளெயின்-கோர்டான் சமன்பாடு (Klein-Gordon Eqn) என அமையும்.

பின்பு நேரியற் அணிக் கோட்பாட்டின் மூலம்,  (-i \hbar \partial^\mu \gamma_\mu -mc )\psi = 0 என டிராக் சமன்பாட்டை எழுதலாம்.

(Dirac Equation \partial^\mu, \gamma_\mu என்பன முறையே 4(பரிமாண)-செயலிகள்,  டிராக் \gamma அணிகள் )

சமன்பாடுகளின் நுட்பங்கள் தற்பொழுது தேவையில்லாதது.  ஆனால் அதன் படிகளைக் காண்க.  டிராக் சமன்பாடு வெறும் ஒருபடிச் சமன்பாடு..  (^\mu என்பது படியல்ல.. அது வெற்றுக் குறி (Einstein Summation index or dummy index)).  இச்சமன்பாட்டின் மூலம், குவாண்ட இயற்கணிதத்தின் அடிப்படைக்கல் நாட்டப்பட்டது.

இந்த சமன்பாட்டின் விளைவால், பாசிட்டிரான் எனும் எதிர்துகள் உதித்தது!  இது எதிர்மத்துகளின் அடிப்படையை விதைத்தது! பாசிட்டிரான்,  எலக்றானின் எதிர்மத்துகள்!  அதாவது பாசிட்டிரானின் சக்தி–எதிர்ம அளவில் இருந்தது Negative energy — இது அவருடையக் காலத்தில், இயற்கைக்குப் புறம்பானவொன்று!  ஆயினும் எண்ணியல் தொடர்புகள் பல,  இயற்கையில், பற்பல விளைவுகளில் இருப்பதைக் காண முடிந்ததைப் போல், போஸ்-ஐன்ஸ்டைன் குளிர்வித்தலில் எதிர்ம சக்தியின் நிரூபணத்தை ஆய்வின் வழிக் கண்டறிந்துள்ளனர்.   இங்கு பயன்பாடு — கோட்பாடாக்கப் பட்டுள்ளது!

பேராசிரியர் செல்வக்குமார் உட்பதி தொகை மின்சுற்றுக் கணக்கீடுகளில் இருபடிகள் இல்லாமலும், வர்க்கமூலம் இல்லாமலும் பயன்படுத்த வேண்டியதைக் குறிப்பிட்டிருந்தார் [4].   அந்தத் தளத்தில் பௌத்தயானரின் சூத்திரத்தையும் விவாதித்துள்ளனர்!

பழங்கால விற்பன்னர்கள்

பாரதத்தின் பண்பாடு மற்றும் தேடலின் சேகரங்களைக் கற்றலின் பொருட்டு பிறநாட்டினர் பயணக்குறிப்புகளில் பகிர்ந்துள்ளதாய் வரலாறு உள்ளன.  அக்குறிப்புகளில் பல, மந்திர தந்திர அல்லது அப்பொழுது இருந்த மாயவித்தைகள் என நிறைய விசயங்களை சந்தேகக்கண் கொண்டு நோக்கினாலும், தத்துவம் சார்ந்த அறிவுப் பரிமாற்றங்கள் வெவ்வேறு அளவுகளில் நடந்துள்ளது உண்மை.   நாம் எப்படி கணிதத்தையும் அறிவியலையும் மதம் சார்ந்த அல்லது சடங்குகள் சார்ந்த ஒரு விசயமாக உருவாக்கினோமோ, உலகின் பிற பகுதிகளிலும் அக்கால அறிவியல் அதே அளவில் நடந்தேறியதையும் அவ்வப்போதுக் காண முடிகிறது.

நான் இவற்றைப் பார்த்துப் பூரிப்பதோ தவிர்ப்பதோ இல்லை, முடிந்தால் உடனே என்னவென்று ஆய்வேன், அல்லது கிடப்பில் கிடக்கும்!  ஆயினும், ஒரு வேலையை, நாம் தற்போது செய்வது போல், பழங்காலத்து ஆட்களால் செய்ய முடியாது அல்லது வேறு மாதிரி செய்வார்கள், அதே போல் தான் நவீன அறிவியலைக் கொண்டு காணும் நமக்கும் பழங்காலத்து ஆட்களைப் போல் சிந்திக்க முடியாது, ஆயினும் அதே மாதிரியான சிந்தனையின் முக்கியத்துவம் பார்க்கப்பட வேண்டுமா என்பது சூழலையும் தேவையையும் பொறுத்தது.

வரலாற்று ஆய்வுகளின் முக்கியத்துவம்

ஆனால், பெரும்பாலானத் தருணங்களில்,  பிரச்சினை என்னவென்றால், அவல் தின்பது போல் வரலாற்றை மெல்லுவது தான்.  அறிவியல் மற்றும் கணித வரலாற்றைப் பற்றி தற்போது உள்ள விஞ்ஞானிகள் கண்டுகொள்வதில்லை எனப் பலர் கவலை கொண்டுள்ளனர்.

ஏற்கனவே, அறிவியல் ஆய்வுகளை, பண்டைய, புதிய என வரையறைகளில் பெரும்பாலும், மேற்கத்திய தத்துவங்களிலேயே வைத்துள்ளனர்.  ஆசிய தத்துவங்கள் அடர்வான சாரங்களைப் பெற்றிருந்தாலும், அவற்றை ஏற்றுக் கொள்வதில் மிகப் பெரிய சுணக்கம் உள்ளது.   நேர்மையாக முன்னெடுத்துச் செல்வோரின் அளவுக் குறைவாய் இருப்பதே இதற்கு காரணம்.  சனரஞ்சகமாகவே, அரிஸ்டாட்டில், சாக்ரடீஸ் தத்துவப்பள்ளிகளைப் பற்றி பெரும்பாலானோருக்குத் தெரியும், ஏன் அரிஸ்டாட்டிலுக்கும் முந்தைய பள்ளிகள் கூட சனரஞ்சகமாக அறியப்பட்டுள்ளன!  ஆனால், மாவீரர், பௌத்தர், பாணினி, தக்கசீலப் பல்கலையின் அருமையைப் பற்றி நம்மவர்களுக்கேப் பெரிதும் தெரிவதில்லை.    அப்படி அறியக் கொணர்ந்தாலும்,  இன்ன அளவு என்றில்லாமல் பெரும்புகழ்ச்சிக்கு ஆட்படுத்துவது.. இல்லை, அவை எல்லாம் மதம் சார்ந்தவை என மேம்போக்காகப் பேசுவது என அறவே சம்பந்தமில்லாத எதிரெதிர் இரட்டை நிலைகளுக்குள் சிக்கிக் கொள்வதாக இருப்பது.

பெருமைக்குட்படுத்துதலோடு ஆய்வுக்குட்படுத்துதலும்!

உதாரணத்திற்கு, பிரையான் ஜோசப்சன் எனப்படும் இயற்பியலர், தனது முனைவர் பட்ட ஆய்வின் போது, கண்டறிந்த மீக்கடத்தி சந்தி (Josephson Junction) என்பதைக் கண்டறிந்தார், அது மிகப் பெரியக் கண்டுபிடிப்பு, அவருடைய 25 வயதிலேயே அதற்காக நோபல் பரிசைப் பெற்றார்!  ஆயினும், தற்போது அவருடையக் கட்டுரைகள் பெரும்பாலும், மனதையும் பருப்பொருளையும் (mind-matter) சார்ந்து எழுதும் ஆய்வுக் கட்டுரைகளை, பெரும்பாலானோர் ஒத்துக் கொள்வதில்லை.  ஆர்கைவ் (arXiv) எனப்படும், ஆய்வுக்கட்டுரைகள் எளிதாக எல்லோரையும் சென்றடையச் செய்யும் வகையில் உருவாக்கப்பட்டத் தளம் கூட, அவருடைய சிலக் குறிப்பிட்ட ஆய்வுகளை ஒதுக்கி வைக்கின்றன!  இதில் மூன்று விசயங்களை உணர வேண்டும்!

  1.  அவர் நோபல் பரிசு பெற்றவர் என்பதாலேயே அவருடையவை எல்லா ஆய்வுகளும் ஏற்கப்படவில்லை யென்பது. (நாம் உயர்வு நவில்பவர்கள், ஆயிற்றா?!! )
  2. அப்படி ஒதுக்கி வைப்பது சரிதானா என்பதைப் பற்றியும் விவாதங்கள் நடந்த வண்ணம் உள்ளன.  அதாவது
    •  ஆய்வின் போக்கை, தாம் கொண்ட அறிவை மட்டும் வைத்து, இது சரி அல்லது தவறு என்று சொல்வது சரிதானா என்பது.  அதாவது ஆய்வின் சுதந்திரத்தை அது பறித்துவிடும்.
    • அதற்கான வடிகாலைக் கட்டமைப்பது. (உதாரணம் viXra, அதாவது arXiv-இன் தலைகீழ்! ஆனால் பல முரணானக் கட்டுரைகள் உள்ளன இதில்!)
  3.  இன்னும் ஜோசப்சன்னின் மற்ற ஆய்வுகள் சரியாக அலசப்பட்டு பிரசுரிக்கப்படவும் செய்கிறது.

 

சங்கப்பலகை அனல் புனல்வாதங்கள்!

ஒவ்வொரு கலாச்சாரமும் ஒவ்வொரு மனிதருக்கான வரையறையை வைக்கிறது.  ஆனால், நம்மவர்கள் பெரும்பாலும், அடுத்த நாட்டினரின் பண்பாட்டு உளவியலுக்குள் தத்தம் தலைகளைப் புகுத்த முயற்சிக்கிறார்கள், அதுவும் மிகவும் ஆகவே ஆகாத விசயங்களில்!   அனல்வாதம் புனல்வாதம் என்பது உவமைகளாக இருந்திருந்தால்,  சங்கப் பலகை-பொற்றாமரைக்குளம் என்பவை எல்லாம்  அக்காலத்தைய, editorial board-இன் ஒப்புமைவடிவம்!  வாதங்கள் எல்லாம் தத்துவங்களின் அலசல் –சமூகத்தால் ஏற்கப்பட்ட வடிவத்தைத் தரும் peer-reviewing system.    எல்லாத் தத்துவப் பின்னணி கொண்ட கலாச்சாரத்திலும், இது போன்ற தராசுகள் இருந்திருக்கின்றன.   சில நேரங்களில், வரலாற்றுப் படிமங்கள் கூறுவது போல், அவை கொஞ்சம் கொடுமையாக, யோசிப்போருக்கு நஞ்சையும் புகட்டியிருக்கின்றன, கழுவிலும் ஏற்றியிருக்கின்றன, கல்லைக்கட்டிக் கடலிலும் இறக்கியிருக்கின்றன.

அரைகுறை முன்னோர் புகழ்ச்சியால், உண்மையான வரலாற்றை நாம் தொலைத்துவிடக் கூடாது.  இது முதல் படி, ஆனால், இது மட்டும் போதாது, சரியான வரலாற்றைப் பதிவும் செய்ய வேண்டும். மகிழ்ச்சியான விசயம் என்னவென்றால், பல விஞ்ஞான நண்பர்கள் கிரேக்கத்துக்கும் முந்தைய அறிவியலில் ஆர்வங்கொள்வதும் நடுநிலையோடு இந்திய அறிவியல் வரலாற்றைப் பற்றி பகிர்வதும் ஆகும், ஆனால் மிகக் குறைவான பேர்களே இவ்வேலையை செய்து வருகின்றனர். என்பதும், அவர்களின் பகிர்வுகள் எவ்வளவு சனரஞ்சகமாக எடுக்கப்படுகிறது என்பதைக் காணும் போது அது வருத்தத்திற்குரிய அளவிலேயே உள்ளது.

ஆனால் அறிவியலுக்கும் கட்டுக்கதைப் புனைந்து புல்லுருவியைப் போல் செய்திகளைப் பரப்பி உளுக்கச் செய்தல், கடைந்தெடுத்த முட்டாள்தனம்.

உசாவுத்துணைகள்:

[1] https://archive.org/details/balagzone_gmail

[2] https://www.facebook.com/photo.php?fbid=10207381186028991&set=rpd.1266837112&type=3&theater

[3] https://drive.google.com/file/d/0BzwpbxABzaV5V0lxS0dZeTFhOGM

[4] http://forums.parallax.com/discussion/147522/dog-leg-hypotenuse-approximation

[5] முடிவிலா மின் சுற்றும், கொஞ்சம் ஜனரஞ்சக திண்ம அறிவியலும்!

 

நிரந்தர அண்டக் கோட்பாடு- இறைவன் – விவாதம்

Posted on by
Reply

இராய் சௌதுரி சமன்பாடு (Raychaudhuri equation) என்பது ஆரம்பமும் முடிவும் இலாத அண்டத்தைப் பற்றியது.  அதனடிப்படையில் இராய் சௌதுரியின் மாணாக்கரான சூர்ய தாஸ் அவர்களின் ஆய்வைப் பற்றி வந்த செய்தியை [1]மொழியியல் பேராசிரியர். தெய்வசுந்தரம் அவர்கள் பகிர்ந்ததனால் விளைந்த விவாதம் இது.

அண்டத்தின் அடிப்படையை, ஈர்ப்பியல் மற்றும் இழைக் கோட்பாடுகள் வழியாக பார்க்கலாம் என நினைக்கிறார்கள். குவாண்டம் ஈர்ப்பியல், இழைக் கோட்பாடுகள் சார்ந்த அளவீடுகளைக் காண சரியானக் கருவிகள் நம்மிடம் இல்லை. அதாவது, அப்படிக் கருவிகள் இருக்கும் பட்சத்தில், அக்கருவிகளே, இயற்கையின் மீச்சிறு அல்லது மீப்பெரு அளவுகளைக் கண்டறியக்கூடியனவாக (எ.கா. மீச்சிறு நேரம் 10^{-50} நொடிகள், பேரண்ட மாறிலி 10^{-123}, கருந்துளை அடர்த்தி 10^{+100}\, kg/m^3— எல்லாம் தோராய அளவுகள்!) இருக்கும். இதற்கு மறைமுக அர்த்தம், நம்மால் அம்மாதிரியானக் கருவிகளை உருவாக்க முடியாது!

மேலும், தற்பொழுதுள்ள இயற்பியற் கோட்பாடுகளின் அடிப்படையில், இம்மாதிரியான அடிப்படைக் கேள்விகளைக் கேட்கும் போது, அடிமனதில் ஒருவித விழிப்புணர்வுடனேயே அணுகும், ஏனெனில் எந்நேரமும் கட்டமைக்கப்பட்ட இயற்பியல் உடைபடலாம் என்பதே ஆகும்! நண்பர் ஒருவர் சொன்னது போல், ஊகங்கள் என்பது வெற்று யோசனைகள் அளவிலானவை கிடையாது, சில ஆய்வுகளில் வெற்றிகளைக் காணும் ஒரு கோட்பாட்டை, அவ்வெற்றிகளைத்தாண்டி/புரிதலைத் தாண்டி அங்கிட்டும் இங்கிட்டும் நீட்டியமைத்தால், பல விதங்களில் புதிய விடைகள் கிடைக்கும். அதனடிப்படையில் ஆனது தான் இது. ஸ்டெடி ஸ்டேட் அல்லது நிரந்தர அண்டக் கோட்பாடு ஒரு பக்கம், பெருவெடிப்பு, பெருங்குறுக்கக் கொள்கையைத் தாண்டி ஓடிக் கொண்டிருக்கிறது!

பேரா. தெய்வசுந்தரம்: ” அனைத்துமே பல பருண்மையான தரவுகள் ( material basis) அடிப்படையில்தான் முன்வைக்கப்படுகின்றன. அத்தரவுகள் , கணிதத்தையும் பிற அறிவியல்துறைகளின் அடிப்படைகளையும் கொண்டு அறிவியல் அறிஞர்களால் விளக்கப்படுகின்றன. அந்த விளக்கங்களில் சில ஊகங்கள் ( hypotheses) முன்வைக்கப்படுகின்றன. இந்த ஊகங்கள் எல்லாம் வெறுமையிலிருந்து (from “nothing”) உருவாக்கப்படவில்லை. இந்த ஊகங்களுக்கு இடையே வேறுபாடுகள் இருக்கலாம். அண்டத்தின் பண்புகள் பற்றி … இன்றுவரை வைக்கப்பட்டிருகிற ஊகங்கள் அனைத்தும் …. (எனக்குப் புரிந்தவரையில்) அண்டத்திற்கு ”படைப்பாளி” … ”இயக்குநர்” இல்லை என்பதைத் தெளிவுபடுத்துகிறது.”

Material basis என்பது சற்று இடறக் கூடியது, உதாரணத்திற்கு குவாண்ட புலக் கோட்பாட்டின் அடிப்படையே, வெற்றிடத்தில் ஏற்படும் அதிர்வுகளின் விளைவுகள் தாம். மேலும், இழைக் கோட்பாட்டிலும், அடிப்படைப் பருப்பொருளாக இழையைக் கொண்டாலும். அதுவும் ஒரு குறியீடு தான், மற்றபடி அதன் பரிமாணம் ஆற்றலாலானது. பெருவெடிப்புக் கொள்கை எனக் கொண்டாலும், ஆதிப்புள்ளியில் அனைத்தும் சக்தி வடிவமாகத் தான் இருந்தது. திரும்பவும் ஆதிப்புள்ளியில் உள்ளப் பிரச்சினை–singularity எனப்படும் முடிவிலி. நமக்கு வெடிப்புக்கு அப்புறம் ஒவ்வொரு நொடியிலும் என்னென்ன உருவாகியிருக்கும் என ஓரளவுக்கு ஊகிக்க முடிவதற்கு காரணம், தற்பொழுதுள்ள அண்டத்தில், நம்மால் உணரப்பட்ட விதிகள். இது ஒருப் பக்கம்.

நாகார்ச்சுனர் (மூலமத்தியம காரிகை) போன்ற தத்துவவியலாளர்கள், வெறுமையின் நீள அகலங்களைக் காணச் செய்த முயற்சிகளையும் நம்மால் காண முடிகிறது. குவாண்டவியலின் கட்டமைப்பும், அதன் முடிவுகளில்-அறுதியற்றத் தன்மையும் வெவ்வேறு விளக்கங்களைத் தேடுவதற்கான வாய்ப்புகளை இன்னும் திறந்தே வைத்திருக்கிறது. உடலில் புரதச்சேர்க்கை நிகழும் அளவில் கூட, ஐசன்பர்க்கின் அறுதியற்ற முடிவுகளைத் தற்பொழுது காண முடிகிறது, என கடந்த வார ஆய்வுக்கட்டுரை ஒன்று விளக்குகிறது. இதன் பொருள், நாம் ஏற்கனவே குவாண்டவியலின் கரைகளில்/எல்லைகளில் நடக்க ஆரம்பித்துவிட்டோம் எனினும் அதன் எல்லைகளை உடைக்கவியலுமா எனத் தெரியவில்லை. இது இன்னொருப் பக்கம்.

இறைவனின் இருப்பை இவற்றை வைத்து சொல்ல இயலுமா என்பது மிகவும் கடினமானக் கேள்வி. இப்படி அண்டசராசரத்தை பெரிய அளவில் நாம் பேசினாலும், பெரும்பொருள் இயற்பியலிலேயே (classical physics) பல புரிந்து கொள்ள முடியாதத் தன்மையுடன் உள்ளன. வெறும் தனி ஊசலின் அலைவைப் புரிந்து கொள்வதற்கு கடுமையானக் கணக்கீடுகளும் ஆற்றல் கொண்டக் கணினிகளின் தேவைகளும் உள்ளன. இறையின் அம்சத்தை மிகப் பெரிதாகக் கொண்டால், நாம் உணர்ந்த விதிகள் அனைத்தும் சிலப் பண்புகளை அளந்து அதனால் விளைந்த அறிவில் இருந்து பெறப்பட்டனவே. அதாவது, முழுமையானப் புரிதல் என்பது நிறையநேரங்களில் தேவைப்படாது. முகநூலைப் பயன்படுத்துவதற்கு, உலாவி, அது இயங்கும் செயலி, அதன் பின் செயல்படும் எலெக்ரானிக்ஸ் என அதையும் அறியத் தேவையில்லை. ஆனால், உயர்நிலையில் அண்டம் பற்றி ஆய்வுசெய்வோர்கள் கூட இப்படி மீச்சிறு அளவில், மிக சிலப் பண்புகளை மட்டுமே வைத்து இவ்வண்டத்தின் நிலைகளை ஆய்வு செய்கிறோம். இதன் அடிப்படையில் காண்கையில் இயக்குனர் பற்றியக் கேள்விக்கு நம்மால் பெரிய அளவில் பதிலளிக்க முடியுமா எனத் தெரியவில்லை. ஹாகிங் அவர்கள் அவ்வப்போது இது சார்ந்து சிலக் கருத்துகளைக் கூறுகிறார்கள், அதில் நான் புரிந்தவரையில், ஒரு பொருளின் தன்மையினை, ஒரு சிலப் பண்புகளை வைத்தே, அப்பொருளைப் பற்றி முழுவதுமாக ஊகிக்க முடிகின்ற பொழுது, நம் இயற்பியலும் கணிதமும் சரியானப் பாதையில் செல்கிறது எனப் பொருள், அப்படியிருக்கும் பட்சத்தில் இயக்குனரின் தேவை எவ்வகையானது என்பதாக இருக்கலாம். ஆயினும் அவருடைய சிலக் கருத்துகள், அவருடைய சொந்த வாழ்க்கையின் அடிப்படையிலும் உள்ளது, அதை அவ்வளவுக்கே எடுத்துக் கொள்ள முடியும் என நினைக்கிறேன்.

உதாரணத்திற்கு, ஏரியில் தவளைக் கல்லெறிதல் [2], செல்டிக் கல்லின் இயக்கம் [3], மிதிவண்டியின் இயக்கம் [4] இப்படி சிறுசிறு விசயங்களில் கூட பெரிய அளவில் இயற்பியல் உள்ளது, அவை அதிசயிக்கத்தக்க வகையில் நமக்குத் தெரிந்த இயற்பியல் விதிகளுக்குட்பட்டே இயங்குகின்றன. அதாவது, இப்படி ஒவ்வொரு விசயத்திலும் அந்தந்த இயக்கத்தைப் புரிந்து கொள்ள முயற்சி செய்யும் பொழுது, ஏதாவதொன்றில், இயற்பியலின் விதிகள் திருத்தியமைக்கப்படலாம். எப்பொழுதும் பரிநிர்வாணநிலையில் இருப்பதே நமக்கு நல்லது எனத் தோன்றுகிறது! 😀

தெய்வ சுந்தரம் நயினார் // Material basis என்பது சற்று இடறக் கூடியது,……. ஆதிப்புள்ளியில் அனைத்தும் சக்தி வடிவமாகத் தான் இருந்தது. // என்று நண்பர் நாகேஸ்வரன் ஈஸ்வர் கூறியுள்ளார். நான் பருண்மை (material) என்று கூறுவது…. இயங்கியல் பொருள்முதல்வாதத் தத்துவத்தில் கூறக்கூடிய பருண்மை அல்லது பருப்பொருள்.. இதற்கு அவர்கள் அளிக்கும் விளக்கம்….. நமது மனதிற்கு … புலனறிவுக்கு வெளியே …. புறவயமாக. ( Objective reality) … நமது மனத்தைச் சாராமல்…. நாம் நினைப்பதால் அது இல்லாமல், மாறாக அது இருப்பதால் நாம் அதை நினைக்கிற ( reflected in our mind) .. ஒன்றே பருண்மைத் தன்மை என்பதாகும்… எனவே சக்தி (energy) என்பதும் பருண்மைத் தன்மை உடையதே. அந்த சக்தியானது இயற்பியலில் கூறக்கூடிய பொருள்திணிவு (mass), இடம் (space ), காலம் (time) ஆகியவை உள்ள பொருளாக ஒரு காலகட்டத்தில் மாறியுள்ளது. அந்த சக்தியில் ஏற்பட்ட மாற்றம்தான் இது. வெறுமையில் (nothing) இருந்து அது தோன்றவில்லை.

தாங்கள் கூறுவது விளங்குகிறது… நான் பேச விழைவது, ontological realism, அது பார்வையாளரின் மனது அல்லது இருப்பைத் தாண்டியது. வெறுமையில் ஏற்படும் மாற்றம் எனவொன்றைக் காண இயன்றால் மிகவும் நன்றாக இருக்கும், உதாரணத்திற்கு காஸிமிர்-போல்டர் விளைவு போல். ஆயினும், இது பெருவெடிப்புக்கு அடுத்த நிலையே அதாவது, நம் இயற்பியல் விதியின் அடிப்படையில் இயங்கும் ஒன்று!

அதே போல் தாங்கள் சொல்லும் வெறுமையில் இருந்து வந்திருக்க இயலாது என்பதும் நாம் உணர்ந்த விதியின் அடிப்படையில் நாம் யோசிப்பதால் விளைவது. அதனால் தான் நான் விதிகளை உடைப்பதையோ விதிகளை மாற்றுவதையோப் பற்றிக் குறிப்பிடுகிறேன். இதில் இன்னொரு ஆர்வத்தைத் தூண்டக்கூடிய ஒன்று , எனக்குப் பிடித்த சீனோ (Zeno of Elea) தோற்றமுரண்கள்.. அதிலும் நேரம் சார்ந்த முரண். அதாவது, மாறக்கூடிய ஒன்றை, மாறாததாகவே/ மாறாதது போல் இருக்கச் செய்வது. இதுவும் தெரிந்த தத்துவ விதிகளுக்கு உட்பட்டது தான், இருந்தாலும், நினைப்பதற்கு மாறான (counter-intuitive) விசயங்களை உள்ளடக்கியது. இங்கு மாற்றத்தின் அளவானது மாறுகிறது. இதையும் Gödel incompleteness theorem தாங்கிக் கொள்வதும் ஆச்சரியமானது. (எனினும், இந்த வாக்கியத்தை, தத்துவ நோக்கில், தீவிர ஆய்வுக்குட்படுத்த வேண்டும்). தங்களுடைய வெறுமையின் வரையறை பெருவெடிப்புக்குப் பிந்தையது, முந்தைய சக்தி பின்னர் மாறிப் பருப்பொருள் ஆக மாறிவுள்ளது என்பதாக உள்ளது. முந்தைய ஆதிசக்தியின் வடிவம் பற்றிய இயற்பியல் நம்மால் உருவாக்க இயலவில்லை, ஆதலால் முற்றுமுழுதாக முன்னிருந்த அனைத்துக்கும், வெடிப்புக்குப் பிந்தைய நிகழ்வுகளின் வழியாக பதில் தெரியுமாவெனத் தெரியவில்லை.

மேலும் எதிர்மத்துகள்களின் அளவு வேறுபாடு ஒரு சின்ன குறை, இது ஒன்று மற்றொன்றாக மாறும் போது சீரில்லாமல் நடந்ததையும் குறிப்பிடுகிறது. எப்படியாயினும், நான் குறிப்பிடுவன குவாண்ட வெறுமை, இழையதிர்வுகள், மற்றொருவகையில் ஒன்றுமில்லாத வெறுமை, அதாவது, வெளிகூட இல்லாதநிலை எனக் கொள்ளலாம், ஆனால் இந்த இரண்டாவது வெறுமை பற்றிய வாதம் மிகவும் அர்த்தமற்றதாகக் காணலாம், தற்பொழுதுள்ள விதிகளின் பிரகாரம், இருப்பினும் சந்தேகத்தின் அடிப்படையில் அதை வைத்திருக்கிறேன்.

[1] http://phys.org/news/2015-02-big-quantum-equation-universe.html
http://arxiv.org/pdf/1404.3093v3.pdf    Cosmology from quantum potential
http://arxiv.org/pdf/1411.0753v3.pdf    Dark matter and dark energy from Bose-Einstein Condensate

[2] http://www.nature.com/news/1998/031229/full/news031229-8.html

[3] http://www.nature.com/news/the-bicycle-problem-that-nearly-broke-mathematics-1.20281?WT.mc_id=FBK_NA_1607_NEWSFBICYCLEPROBLEM_PORTFOLIO

[4] http://arxiv.org/abs/1202.6506

கற்றலும் சமூகமும் – 1: பள்ளிக் கல்வியமைப்பும் சூழலும்

Posted on by
2

பாடத்திட்டத்தை வடிவமைப்பதில் உள்ள சிக்கல்களையும், உயர்கல்விக்குத் தேவையானக் கூறுகள் அனைத்தும் பள்ளிக்கல்வியில்- சாதாரணப் பாடத்திட்டத்தில்- அமையவில்லையா எனவும் நடந்தவொரு விவாதத்தில், தோன்றியக் கருத்து.   வெவ்வேறு வகையான நோக்கில் இதே விசயத்தை நான் பகிர வாய்ப்புகளுண்டு.

பெரும்பாலான ஐஐடி மாணாக்கர்கள், தங்களின் ஆர்வத்தாலோ, பெற்றோர்களின் உந்துதலாலோ தான் வருகிறார்கள், எப்படியிருப்பினும், அவ்வாறு வருபவர்கள், பள்ளிக் கல்வியளவிலான பாடத்திட்டங்களுடன் உள்ளே நுழைவதில்லை, பள்ளிக் கல்வியளவிலான அறிவு போதுமானதாக இருந்தாலும், சிறிய கால இடைவெளியில் நடைபெறும் பரீட்சையில், அதே நேரம் பிழிந்தெடுக்கும் அளவிலான நுழைவுத்தேர்வுகளில், அவை உதவாது. ஆக படிப்பது என்பது திணித்தலாகவோ, அல்லது விரும்பிப் படிப்பதாகவோ அமையும். ஆயினும், பாடங்களை இது மாதிரியான தேர்வுகளுக்கு சொல்லிக் கொடுக்கும் விதமும் பெரிதாக மாறுபடும். பள்ளியளவிலானத் தேர்வுக்கு, கல்லூரியளவிலான பாடத்திட்டங்களுடன் தயார் ஆக வேண்டியிருக்கவும் செய்யலாம். உதாரணத்துக்கு, ரெஸ்னிக் & ஹாலிடே இயற்பியல், விட்டர் உயர் நுண்கணிதம், கல்லூரி இயற்கணிதம் இது போல.

என்னுடையப் பள்ளிக் கல்வியின் போது, +2வுக்கு கணிதம் எடுப்பவர்கள் ஒரு டெம்ப்ளேட் போல் எடுத்துச் சென்றுவிடுவர், எங்கிருந்து வந்தது என்றெல்லாம் கேட்க முடியாது. இன்னும் அவ்வாறே இருக்கும் பட்சத்தில், மதிப்பெண்களால் கட்ட்மைக்கப்பட வேண்டியிருக்கும் சமூகத்தில் அல்லது அவ்வளவு பயிற்சிப் போதுமெனில் பிரச்சினையில்லை. ஆனால், வேட்கை கொண்ட மாணவனுக்கு அதற்கான வழிமுறைகளும் இருந்தால் நலம். இருப்பினும், பிரச்சினை, போதுமான தூண்டுதல் முயற்சிகள் நடக்கின்றனவா என்பது தான். எதற்காகப் படிக்கிறோம் என்பதற்கு முழுமையான பதில் தரமுடியவில்லையெனினும், தாகங்கொண்ட மாணவர் சமுதாயத்தை உருவாக்க வேண்டியது அவசியம்.  உதாரணத்துக்கு, என்னுடைய அமெரிக்க ஆய்வு நண்பர், நம்முடையப் பள்ளியளவிலேயே, நாம் வகைக்கெழு சமன்பாடுகளைப் (differential equations ) படிப்பதை ஆச்சரியமாகக் குறிப்பிட்டார். அவர்கள் அப்படிப் படிப்பதில்லையெனினும், நல்ல ஆய்வாளர்களாகத் தான் இருக்கிறார்கள். அதே போல் படிக்கும் நம்மவர்கள் பெரும்பாலும், அதைப் பற்றித் தெரிந்து கொள்ள விரும்புவதுமில்லை.

NCERT புத்தகங்களை வடிவமைப்பது பெரும்பாலும், ஐஐடி ஐஐஎஸ்சி ஆர்ஐஈ போன்ற நிறுவனப் பேராசிரியர்கள், அவை ஆரம்பப்பள்ளிப் பாடத்திட்டங்கள் என்றாலும்! ஆக நம்மிடம் இருப்பது நல்ல அமைப்புகள் தாம், ஆனால் அதை சரிவர பயன்படுத்தத் தெரியாமலும் இருக்கிறோம். இவற்றைத் தெரிந்தவர்களுக்கு எடுத்துக் கூறினாலும், இதை வைத்து நிறைய மதிப்பெண்கள் வருமா எனக் கேட்கிறார்கள், அதோடு நின்றாலும் பரவாயில்லை, அப்படியே “நம் கல்விமுறையே சரியில்லை” என்று வைது புலம்பவும் செய்கின்றனர்.